 Casi metido de lleno en época de exámenes se me ha ocurrido traer hasta aquí al conocido problema de Monty Hall. Dicho problema recibe este nombre porque aparecía en el programa televisivo estadounidense Let's Make a Deal (Hagamos un trato) que presentaba el propio Monty Hall. Este programa dio lugar a una cuestión que provocó revuelo y discusiones entre los más famosos matemáticos del momento y hoy día se ve como un claro ejemplo de que la intuición humana en ocasiones es errónea.
Casi metido de lleno en época de exámenes se me ha ocurrido traer hasta aquí al conocido problema de Monty Hall. Dicho problema recibe este nombre porque aparecía en el programa televisivo estadounidense Let's Make a Deal (Hagamos un trato) que presentaba el propio Monty Hall. Este programa dio lugar a una cuestión que provocó revuelo y discusiones entre los más famosos matemáticos del momento y hoy día se ve como un claro ejemplo de que la intuición humana en ocasiones es errónea.Veamos una descripción de este problema:
Se le muestran al concursante tres puertas cerradas: A, B y C. Sólo una puerta esconde el premio del concurso (que es un coche) mientras que en cada una de las otras dos hay una cabra. El presentador conoce que hay detrás de cada puerta (cabra o coche).
El concursante elige una de las tres puertas posibles. Seguidamente, una de las dos puertas que el concursante no ha escogido es abierta por el presentador y muestra que tras ella hay una cabra. La situación ha cambiado y ahora nos encontramos ante dos puertas que pueden contener una cabra o un coche. Una de estas dos puertas fue inicialmente escogida por el concursante. En términos probabilísticos, ¿debe mantener la puerta elegida en un principio, cambiar su selección inicial o es exactamente igual hacer una cosa u otra?
¿Qué haríais vosotros? Lo cierto es que nuestra lógica ve con claridad que es exactamente lo mismo cambiar de puerta que no hacerlo ya que al quedar sólo dos puertas la probabilidad de llevarnos el coche cambiando nuestra elección es la misma que si la mantenemos, esto es, un 50%. Pero esto es totalmente erróneo. La respuesta correcta es que siempre debemos cambiar la puerta que elegimos inicialmente pues tendremos el doble de opciones de conseguir el coche. ¿Por qué? Llegados a este momento explicaré el motivo desde tres puntos de vista diferentes:
a) Analicemos todos los casos posibles que son sólo tres: elegir inicialmente la puerta que oculta el coche, elegir inicialmente la puerta que oculta la primera cabra o elegir inicialmente la puerta que oculta la segunda cabra:
- Elegimos puerta con coche. El presentador abre una puerta y detrás hay una cabra. Debemos mantener la puerta elegida inicialmente. Mantener puerta 1 - Cambiar puerta 0.
- Elegimos puerta con una cabra. El presentador abre una puerta y detrás está la otra cabra. Debemos cambiar la puerta elegida inicialmente. Mantener puerta 1 - Cambiar puerta 1.
- Elegimos puerta con la otra cabra. El presentador abre una puerta y detrás está la otra cabra. Debemos cambiar la puerta elegida inicialmente. Mantener puerta 1 - Cambiar puerta 2.
b) Cuando inicialmente se elige la puerta, ésta nos da una probabilidad del 33% de contener al coche mientras que el conjunto formado por las otras dos puertas tienen un 66%. Una vez que el presentador abre una de las dos puertas que ocultaban una cabra la probabilidad de que el coche se encuentra en esta puerta pasa a ser cero. Por tanto, si la probabilidad de que el conjunto de las dos puertas no elegidas en un principio contengan al coche es de un 66% y una de ellas posee una probabilidad del 0% (pues ha sido abierta y detrás hay una cabra) entonces la otra puerta (la no escogida y que sigue sin abrir) absorberá la probabilidad que tenía el conjunto formado por las dos puertas no seleccionadas, esto es, un 66%. Veámoslo gráficamente:
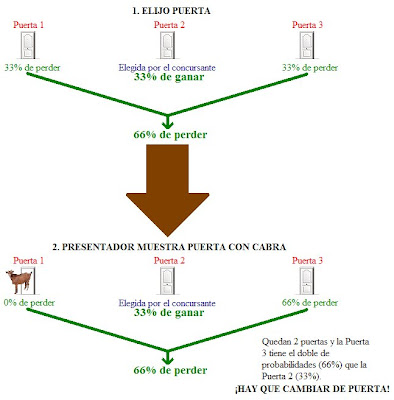
c) Replanteeemos este problema y extrapolémoslo a una situación extremista. Imaginemos que en vez de 3 puertas, disponemos de 1000 puertas y sólo en una de ellas se encuentra el premio deseado, es decir, el coche. En las restantes puertas hay 999 cabras. Elegimos una de entre las 1000 posibles puertas. A continuación, el presentador nos abre todas las puertas excepto dos (al igual que en el caso de las 3 puertas, donde el presentador nos abría todas las puertas excepto dos, es decir, sólo una). Por tanto, el presentador nos abre 998 puertas y detrás de cada una de ellas hay una cabra. Usando la lógica, ¿crees que habrás acertado a la primera entre 1.000 puertas? ¿O más bien piensas que probablemente esté en la única puerta que no hemos elegido y el presentador no ha abierto? Es evidente que lo más probable es que no hayamos acertado a la primera entre 1000 posibilidades y debemos cambiar. Si mantenemos nuestra puerta sólo tendremos un 0,1% de ganar el coche, mientras que si cambiamos habrá un 99,9%.
Si extrapolamos este problema a un número mucho mayor de puertas será más evidente que debemos cambiar. Por ejemplo, si hay un 1.000.000 de puertas es prácticamente imposible que acertemos al principio entre tantas opciones y cuando el presentador nos deje únicamente ante la puerta que elegimos y otra más, si mantienes tu puerta y ganas el coche es que ha ocurrido un milagro.
Espero que os haya convencido con estas tres explicaciones. Siempre hay que cambiar de puerta. Y de todo esto se dio cuenta antes que nadie Marilyn vos Savant, considerada la persona con mayor coeficiente intelectual del planeta (228). Muchos matemáticos le pidieron que diera cuenta de su error y rectificara inmediatamente cuando eran ellos los que finalmente tuvieron que reconocer que su intuición falló.


No hay comentarios:
Publicar un comentario